과대적합을 해결하는 대표적인 방법 중 하나로 가중치 규제(regularization)이 있다. 가중치 규제란 말 그대로 가중치의 값이 커지지 않도록 제한하는 기법이다. 가중치를 규제하면 모델의 일반화 성능이 올라간다.
아래에 간단한 샘플 데이터와 모델 2개를 그래프로 나타내었다. 이 그래프로 가중치 규제를 설명하겠다.

두 그래프 중에 경사가 급한 그래프보다 경사가 낮은 그래프가 박스로 표시한 샘플 데이터를 더 잘표현하기 때문에 경사가 급한 그래프보다는 경사가 완만한 그래프가 성능이 좋다고 평가한다.

하지만 이렇게 샘플 데이터에 딱 맞는 그래프는 샘플 데이터 6개에 너무 집착한 나머지 박스로 표시한 샘플 데이터를 제대로 표현하지 못하고 있다. 모델이 몇 개의 데이터에 집착하면 새로운 데이터에 적응하지 못하므로 좋은 성능을 가졌다고 할 수 없다. 바로 이것을 '모델이 일반화되지 않았다'라고 말한다. 이럴 때 규제를 사용하여 가중치를 제한하면 모델이 몇 개의 데이터에 집착하지 않게 되므로 일반화 성능을 높일 수 있다. 여기서는 대표적인 규제 기법인 L1 규제와 L2 규제를 살펴보고 두 기법을 이전에 구현한 SingleLayer 클래스에 적용해 보겠다. 또 규제를 적용하면 손실 함수의 그래프가 어떻게 변하는지도 분석해 보겠다.
L1 규제
L1 규제는 손실 함수에 가중치의 절댓값인 L1 노름(norm)을 추가한다. L1 노름은 다음과 같이 정의된다.

소문자 알파벳(w)은 벡터를 의미한다.
여기에서 L1노름의 n은 가중치의 개수를 의미하므로 L1 규제를 '가중치의 절댓값을 손실 함수에 더한 것'으로 이해해도 괜찮다. 다음은 로지스틱 손실 함수이다.

이 손실 함수에 L1 노름을 더하면 L1 규제가 만들어진다. 이때 L1 노름을 그냥 더하지 않고 규제의 양을 조절하는 파라미터 a를 곱한 후 더한다.

a는 L1 규제의 양을 조절하는 하이퍼파라미터이다. 예를 들어 a 값이 크면 전체 손실 함수의 값이 커지지 않도록 w값의 합이 작아져야 한다. 이것을 보고 규제가 강해졌다고 한다(가중치가 작아졌으므로). 반대로 a값이 작으면 w의 합이 커져도 손실 함수의 값이 큰 폭으로 커지지 않는다. 즉, 규제가 약해진다.
경사 하강법으로 가중치를 업데이트하기 위하여 L1 규제를 적용한 로지스틱 손실 함수를 미분한다.
L1 규제의 미분
로지스틱 손실 함수의 미분한 식은 -(y-a)x로 이미 알고있다. L1 규제만 미분해 보겠다. 절댓값 |w|를 w에 대해 미분하면 w 값의 부호만 남기 때문에(w가 양수이면 +1, 음수이면 -1)w 값을 미분한 결과인 w의 부호라는 의미로 sign(w)이라고 표현한다. L1 규제를 적용한 손실함수의 도함수는 다음과 같다.

SGDClassifier 클래스에는 penalty 매개변수 값을 l1으로 지정하는 방법으로 L1 규제를 적용할 수 있다.
회귀 모델에도 같은 원리를 적용하여 손실 함수(제곱 오차)에 L1 규제를 적용할 수 있다. 이런 모델을 라쏘(Lasso)라고 부른다. 라쏘는 가중치를 줄이다 못해 일부 가중치를 0으로 만들 수도 있다. 가중치가 0인 특성은 모델에서 사용할 수 없다는 것과 같은 의미이므로 특성을 선택하는 효과를 얻을 수 있다. 사이킷런에서는 sklearn.linear_model.Lasso 클래스에서 라쏘 모델을 제공한다. 미분 결과에서 알 수 있듯이 L1 규제는 규제 하이퍼파라미터 a에 많이 의존한다. 즉, 가중치의 크기에 따라 규제의 양이 변하지 않으므로 규제 효과가 좋다고 할 수 없다.
L2 규제
L2 규제는 손실 함수에 가중치에 대한 L2 노름(norm)의 제곱을 더한다. L2 노름은 다음과 같이 정의된다.

손실 함수에 L2 노름의 제곱을 더하면 L2 규제가 된다. 이때 a는 L1 규제와 마찬가지로 규제의 양을 조절하기 위한 하이퍼파라미터이고 1/2은 미분 결과를 보기 좋게 하기 위하여 추가했다. 여기서도 로지스틱 손실 함수를 사용한다.

L2 규제의 미분
L2 규제를 미분하면 간단히 가중치 벡터 w만 남는다.

L2 규제는 그레이디언트 계산에 가중치의 값 자체가 포함되므로 가중치의 부호만 사용하는 L1 규제보다 조금 더 효과적이다. 또 L2 규제는 가중치를 완전히 0으로 만들지 않는다. 가중치를 완전히 0으로 만들면 특성을 제외하는 효과는 있지만 모델의 복잡도가 떨어진다. 이러한 이유로 L2 규제를 널리 사용한다.
회귀 모델에 L2 규제를 적용한 것을 릿지(Ridge) 모델이라고 한다. 사이킷런에서는 릿지 모델을 sklearn.linear_model.Ridge 클래스로 제공한다. SGDClassifier 클래스에서는 penalty 매개변수를 l2로 지정하여 L2규제를 추가할 수 있다. 두 클래스 모두 규제의 강도는 alpha 매개변수로 제어한다.
L1 규제와 L2 규제 정리
경사 하강법에 규제를 추가하는 방법은 어렵지 않다.
L1 규제는 그레이디언트에서 alpha에 가중치의 부호를 곱하여 그레이디언트에 더하면 된다.
w_grad += alpha * np.sign(w)
L2 규제는 그레이디언트에서 alpha에 가중치를 곱하여 그레이디언트에 더하면 된다.
w_grad += alpha * w
로지스틱 회귀에 규제를 적용
이전에 만든 SingleLayer 클래스에 L1 규제와 L2 규제를 적용하기 위한 코드를 추가하고 위스콘신 유방암 데이터 세트에서 두 규제가 적용된 로지스틱 회귀 모델을 훈련해 보겠다. 보통 실무에서는 규제 효과가 뛰어난 L2 규제를 주로 사용하는데 여기에서는 L1 규제와 L2 규제의 차이점을 알아보기 위해 두 규제를 모두 구현해 보겠다.
먼저 __init__() 메서드에 L1 규제와 L2 규제의 강도를 조절하는 매개변수 l1과 l2를 추가한다. l1과 l2의 기본값은 0이고 이때는 규제를 적용하지 않는다.

다음으로 fit() 메서드에서 역방향 계산을 수행할 때 그레이디언트에 페널티 항의 미분값을 더한다. 이때 L1 규제와 L2 규제를 따로 적용하지 않고 하나의 식으로 작성했다. 즉, L1 규제와 L2 규제를 동시에 수행할 수도 있다.

다음으로 로지스틱 손실 함수 계산에 페널티 항을 추가하겠다. 로지스틱 손실 함수를 계산할 때 페널티 항에 대한 값을 더해야 한다. 이를 위해 reg_loss() 메서드를 SingleLayer 클래스에 추가한다. 이 함수는 훈련 세트의 로지스틱 손실 함수의 값과 검증 세트의 로지스틱 손실 함수의 값을 계산할 때 모두 호출된다.

마지막으로 검증 세트의 손실을 계산하는 update_val_loss() 메서드에서 reg_loss()를 호출하도록 수정한다.

이제 규제를 추가하여 로지스틱 회귀 모델을 훈련해 보겠다. 먼저 L1 규제를 적용한다. L1 규제의 강도에 따라 모델의 학습 곡선과 가중치가 어떻게 바뀌는지 확인해 보겠다. 규제 강도는 0.0001, 0.001, 0.01 이 세가지를 선택하겠다. 다음에 for문을 사용하여 각각 다른 강도의 하이퍼파라미터로 모델을 만들고 학습 곡선과 가중치를 그래프로 나타내었다.

그래프를 보기 좋게 만들기 위하여 맷플롯립의 title() 함수로 제목을 넣고 ylim() 함수로 y축의 범위를 제한했다. 코드를 실행하면 다음과 같은 그래프가 그려지는데 위쪽(Learning Curve)은 학습 곡선 그래프이고, 아래쪽은 가중치(Weight)에 대한 그래프이다.

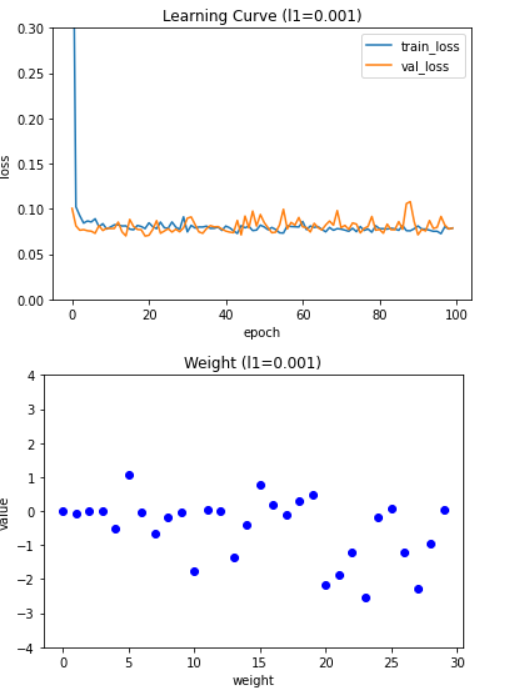

학습 곡선 그래프를 보면 규제가 더 커질수록 훈련 세트의 손실과 검증 세트의 손실이 모두 높아진다. 즉, 과소적합 현상이 나타난다. 가중치 그래프를 보면 규제 강도 l1 값이 커질수록 가중치의 값이 0에 가까워지는 것을 볼 수 있다. 그래프를 보면 적절한 l1 하이퍼파라미터 값은 0.001 정도인 것 같다. 이 값을 사용하여 모델의 성능을 확인해 보겠다.

결과를 보니 규제를 적용하지 않고 검증 세트로 성능을 평가했을 때의 값과 동일하다. 이 데이터 세트는 작기 때문에 규제 효과가 크게 나타나지 않는다. 다음으로 L2 규제를 적용해 보겠다.
l1 때와 같은 방법으로 L2 규제의 강도를 조절하고 모델을 훈련하여 학습 곡선과 가중치를 그래프로 그린 후 확인해 보겠다.
코드를 실행하여 얻은 그래프는 다음과 같다.


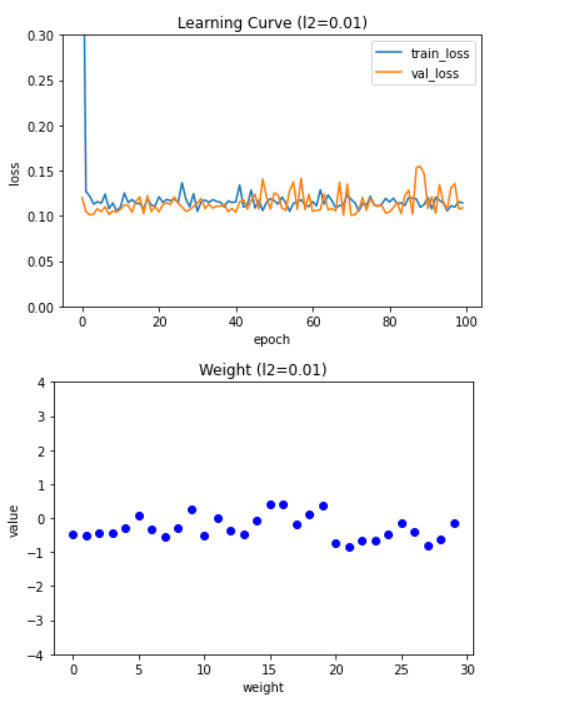
두 그래프를 보면 L2 규제도 L1 규제와 비슷한 양상을 보인다. 하지만 마지막 학습 곡선 그래프를 보면 L2 규제는 규제 강도가 강해져도(l2=0.01) L1 규제만큼 과소적합이 심해지지는 않는다. 가중치 그래프를 보아도 가중치가 0에 너무 가깝게 줄어들지 않는다는 것도 알 수 있다. L2 규제를 적용한 모델 역시 50번의 에포크 횟수만큼 훈련하고 성능을 평가해 보겠다.

결과를 보니 L1 규제와 동일하다. 사실 cancer 데이터 세트의 샘플 개수는 아주 적어서 L1 규제를 적용한 모델과 L2 규제를 적용한 모델의 성능에는 큰 차이가 없다. 다시 말해 두 모델은 모두 검증 샘플에 대하여 옳게 예측한 샘플의 개수가 동일하다. 하지만 L1 규제를 사용했을 때보다 에포크가 크게 늘어났다. L1 규제를 적용할 때는 20번의 에포크 동안 훈련을 했지만 L2 규제를 적용할 때는 50번의 에포크 동안 훈련을 햇다. 가중치를 강하게 제한했기 때문에 검증 세트의 손실값을 일정한 수준으로 유지하면서 알고리즘이 전역 최솟값을 찾는 과정을 오래 반복할 수 있었던 것이다.
사이킷런의 SGDClassifier 클래스도 L1 규제, L2 규제를 지원한다. penalty 매개변수에 l1이나 l2를 매개변수 값으로 전달하고 alpha 매개변수에 규제의 강도를 지정하면 된다. 여기서는 cancer 데이터 세트를 사용하여 SGDClassifier 모델에 L2 규제를 적용해 보겠다.

결괏값은 SingleLayer 클래스의 결과와 동일하다.
사이킷런에는 SGDClassifier 클래스 이외에도 L1 규제와 L2 규제를 지원하는 모델이 많다. 예를 들면 LogisticRegression, SVC, LinearSVC 클래스 등이 있는데, 이 클래스들은 페널티 항대신 주손실 함수의 크기를 조절하기 위해 하이퍼파라미터 C를 곱해준다. SGDClassifier 클래스의 매개변수 alpha를 사용하여 규제를 제어한 것과 비슷하게 매개변수 C를 사용하여 규제를 제어하는 것이다. 이때 C는 alpha의 반대의 역할을 한다. 즉, 매개변수 C가 커지면 규제가 줄어들고 C가 작으면 규제가 강해진다.
'머신러닝&딥러닝 > Do it ! 딥러닝 입문' 카테고리의 다른 글
| 교차 검증 (0) | 2020.12.24 |
|---|---|
| 과대적합과 과소적합 (0) | 2020.12.23 |
| 검증 세트를 나누고 전처리 과정 배우기 (0) | 2020.12.23 |
| 사이킷런으로 로지스틱 회귀 수행하기 (0) | 2020.12.02 |
| 로지스틱 회귀 뉴런으로 단일층 신경망 만들기 (0) | 2020.12.02 |